The following command line was used to stream the Kepler Exoplanet 4 data file into baudline:
cat 2010-01-22-kepler-exo4-1420mhz.dat | baudline -session setiquest -stdin -format s8 -channels 2 -quadrature -flipcomplex -samplerate 8738133 -fftsize 65536 -pause -utc 0
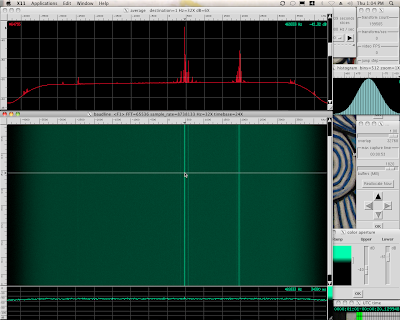
Full 8.738 MHz view
The Kelper Exo4 file was streamed into baudline's standard input. A 65536 point FFT was used for a bin resolution of 266.667 Hz / bin. The Welch window was used for a little more signal extraction SNR. The Histogram window shows a nice Gaussian noise shape with even-odd holes for the 8-bit samples. Optimal anti-alias beam slices were used to smooth the spectrogram and the Color Aperture window was tweaked to maximize the color resolution. Only 50 seconds of the spectrogram are shown because the run was RAM limited. The red Average spectrum shows a hump and 6 strong tones.

From the spectrogram; the two strongest features are the stationary tone at -3874 kHz and the spectral hump at 1000 kHz. Looking at the red Average plot shows several more sharp tones. Here is a list of the potentially interesting targets, add 1419.4464 MHz base frequency:
- -3868800 Hz - very strong - stationary
- -3470933 Hz - strong - random walk - drift
- -2713067 Hz - weak - wild random walk - drift
- -1482667 Hz - strong - wild random walk - drift
- +586133 Hz - strong - drift - extremely interesting - "friend"
- +977867 Hz in hump - weak - wild random walk - drift
- +900000 ... +1111000 Hz (hump) - hydrogen - see below
Hydrogen and Friend
Zooming the Average window into the frequency axis reveals this strong tone and spectral hump. Tone and hump, they make an interesting pair.

The spectral hump at +1 MHz is hydrogen. Interstellar hydrogen in space emits radio frequencies at 1.42 GHz, so with the base frequency offset the hump is centered at around 1.421 GHz. The strong tone to the left is just outside the "water hole" and because it requires a much more detailed analysis we will investigate it last.
-3868800 Hz
Decimating by 4096. Very strong stationary tone in the filter roll-off skirt. No drift. Not interesting.

-3470933 Hz
Decimating by 4096. Random walk tone with positive slope drift. +29 Hz drift / 326 seconds = +0.089 Hz / sec.

-2713067 Hz
Decimating by 4096. Random walk tone with positive slope drift. Difficult to measure, roughly +29 Hz drift / 326 seconds = +0.089 Hz / sec. It looks a bit like the previous signal but it is much weaker and it appears to be jumping around more. It could be a sideband of something but it doesn't seem to be harmonically related to the previous tone. More decimation might help pull out more signal.

-1482667 Hz
Decimating by 4096. Random walk tone with positive slope drift. Difficult to measure, roughly +29 Hz drift / 326 seconds = +0.089 Hz / sec. Looks almost exactly like a stronger version of the above signal.

+977867 Hz
Decimating by 4096. This signal is the weak tone that is in the hydrogen hump mentioned above. Very weak version of the above signal. Strength and random wander are almost identical to the -2713067 Hz signal. Why this signal is in the hydrogen hump is unknown.
 This and the previous two signals are virtual copies of each other. They do not appear to be harmonically related. They could be sidebands or distortion products of the strong stationary tone but the harmonic relationship doesn't seem correct.
This and the previous two signals are virtual copies of each other. They do not appear to be harmonically related. They could be sidebands or distortion products of the strong stationary tone but the harmonic relationship doesn't seem correct.+586133 Hz
"Hydrogen's friend." This signal is extremely interesting. The true frequency of this tone is 1420.586133 MHz and it is just to the left of the hydrogen spectral hump. To zoom into the +586223 Hz tone the Input Devices window was set to decimate by 4096 with a +30 dB gain to improve the quantization SNR.1 The down mixer was set to a center frequency of +586133.3 Hz. The 4096 decimation along with a 65536 point FFT resulted in a bin resolution of 0.0651 Hz / bin.

The red spectrum in the Average window shows a strong +15 dB tone at +586223 Hz. The Histogram window shows the noise to have a nice Gaussian shaped curve. The Gaussian window was used to improve the spectral time resolution. The Color Aperture window was set to a -27 ... -61 dB range to improve the color resolution of the spectrogram. The green spectrogram window shows what previously was a constant stationary tone is now a drifting signal that has a slight random walk. Note that the spectrogram's horizontal zoom has been changed to Hz=1X. Here is a full screenshot:

Making some measurements in the spectrogram window shows that the +586223 Hz signal has a drift of +4.30 Hz / 326 seconds = +0.0132 Hz / second. It starts as what looks like a random walk as the tone zigzags back and forth. Then something really interesting happens half way down, it looks like the signal is being modulated. Zooming in on the lower half and increasing the Gaussian beta value to 11 shows: (click on image for higher resolution version)

This looks like FSK modulation with the delta between mark and space frequencies being about 1.2 Hz. Below is the Average spectrum showing the mark and space frequencies:

The purple spectrum is from the beginning of the modulated section. Since the signal is drifting with a positive slope the mark and space frequencies move to the right. The green spectrum is from the mid/bottom of the modulated section. This is clearly 2-tone FSK but at an extremely low baud rate with a very close mark and space frequency delta.
Enhance Resolution
The new blip Fourier transform enhances spectral resolution which is ideal for deep zooming down to the sample level. Time, frequency, and phase details are improved by using a new analysis primitive called the blip(let). A focus parameter allows for algorithm fine tuning on a signal by space by zoom basis.
Zooming into the FSK signal using a second decimation pass for a total decimate by ratio of 524288 and a bin resolution of 0.01628 Hz / bin. With focus=1 the structure of the individual FSK bits are clearly visible in the magnitude space view below:

Also part of the blip Fourier transform is a blind phase lock algorithm that tracks changes in phase. The problem of spinning phase that is inherent in the short-time Fourier transform (STFT) is solved with blind phase locking. Now the other half of the spectrum, the phase half, contains visibly useful information. With focus=4 the phase of the FSK bits are fairly constant in the unwrapped phase space view below:

The visible phase changes follow what is expected for a random walk coupled with FSK mark/space transitions. There is a fair amount of phase noise present but it does not appear that any phase coding exists within the steady state or the bit transitions.
In the spectrum section above the dB axis is incorrect. Since this is phase space the units should be {-pi ... +pi}. This will be fixed in a future version of baudline.
Also note that the spectrogram timebase parameter for the above images was set to 3X. The overlap value was 1 so this means that baudline can zoom in three more scale factors before the digital bottom is reached at the discrete sample level.
Demodulation
Since the entire FSK signal is drifting somewhat randomly at about +0.0132 Hz/sec machine demodulation is a bit difficult. Backed decimation up a notch from the previous Enhanced Resolution section since the following demodulation works better with a little less zoom. Used a second decimation pass, like was done previously, for a total decimate by ratio of 262144 and a bin resolution of 0.03255 Hz / bin. Baudline's periodicity bars were used to place and fine tune a horizontal grid that perfectly matched the modulated FSK symbols. See the two slightly overlapped spectrograms that have the periodicity bar overlays below: (click on image for higher resolution version)


Note that FSK2 modulation has one symbol per baud. From the periodicity bars delta selected value the baud rate was measured to have a period of 1.976 seconds which is 0.5061 baud. This works out to a spectral efficiency of roughly 0.17 (bit/s)/Hz.2 The periodicity bars sliced the symbols perfectly. With the periodicity bars up I was able to manually demodulate the individual bits. Here are the demodulated bits, it begins with a large number of leading zeroes:
00000000000000000000000000000000000000000000000
10100010001010101010010000000000101010101001010
10101010101010101010101010010101010101010101010
In an attempt to make some sense of this bit stream here are the demodulated bits in a reduction grammar notation:3
0* 2(10) 00 1(10) 00 5(10) 0 1(10) 9(0) 5(10) 0 15(10) 0 10(10)+
where the 0's and 1's are bits and the bit string in parenthesis is repeated by the number before it. The pattern is mostly repeating 10's interspersed with an occasional 0 or two.
Ignoring the leading zeroes, here is the bitstream broken down into 32-bit hexadecimal integers (big endian):
10100010 00101010 10100100 00000000 = 0xA22AA400
10101010 10010101 01010101 01010101 = 0xAA955555
01010101 00101010 10101010 101010.. = 0x552AAAA.
There are 55 zero bits and 39 one bits which is somewhat lopsided but the sample size is way to small for that to be significant. It is interesting that there is not a single run of ones (11) in the bit stream which would suggest some form of Non-Return-to-Zero Inverted (NRZI) coding.4
The bit stream is definitely not random but I haven't been able to decode a pattern out of it yet. It is also possible that the demodulation process produced a couple of bit errors. It is also unfortunate that the data file terminated when it did. Plugging this bit stream (and parts of it) into Google returns zero hits. Maybe some bit wackers5 or crypto folk can pull meaning out of this bit stream.
Listen
The decimated quadrature FSK signal was mixed up to passband (real). To hear this signal download the kepler-exo4_FSK.wav file, load it into baudline, then open the Play Deck window to adjust the audio controls, and press play.

You can slow down the sample rate by adjusting the speed control or change the center down mix frequency by adjusting the shift control. Pressing the small arrow in the bottom right corner will pop down a section that has more controls. From there you can apply an equalization curve or adjust low and high pass filters to remove out-of-band noise.
Autocorrelation
The random walk wandering FSK signal was then ran through baudline's Autocorrelation transform. The Autocorrelation transform shows the self similarity of a signal and it can also be utilized as a form of waveform trigger lock mechanism. Think of Autocorrelation as a sort of self syncing waveform raster display.
For reference the Color Aperture window parameters were set to upper=-48 dB and lower=-69 dB. All other parameters except the windowing function are default. The Kaiser window was used and the beta parameter was increased from 0. to 15. in steps to create the following Autocorrelation spectrogram images:
beta = 0. (square window)

beta = 5.

beta = 15.

The progression of the Kaiser beta value shows how the structure evolves as the window gets narrower. No beta value here is inherently correct but the structures seem to stabilize with the higher betas.
Here is an Autocorrelation movie of the variation of the Kaiser window beta. Notice how patterns and structures pop out of the noise as the beta parameter changes. The audio in the movie is the sound of the drifting random walking FSK signal that has been speed and frequency shift modified for the audio band. Make sure to watch this in fullscreen 720p HD so you can see all the details.
This is not random noise and this is not what the Autocorrelation of a random walk looks like. I was expecting to see the FSK bits flipping on and off from a synchronized waveform perspective. That didn't happen and what this is is a lot more than 94 bits worth of structure. Also the drifting random walk isn't random at all, it contains information. What I believe is happening is that the drifting random walk and the FSK bit stream are modulated together to create this image. I've never heard of a modulation scheme like this before. It does have elements of NTSC and Hellschreiber to it but at an extremely low data rate.
I tried different FFT sizes and different time domain operations from the Input Mapping window that cause various signal distortions. The basic image structure did not change. This tells me that the signal is fairly robust and not an artifact created by the analysis equipment.
Conclusion
The importance of this analysis depends greatly on the identity of the target source. Is it the Kepler satellite, the Kepler-4 planet, or something else? It is very unlikely an error in the collection or analysis caused the modulated bit section because other features in this data file are stationary or drifting differently. It is extremely unlikely that the modulated bits were created by natural phenomena. Decoding of the bit stream may prove enlightening in identifying the source. The Autocorrelation images are likely an interesting byproduct of the FSK data stream coupled with the drifting random walk.
I really don't know what to say or think at this point. The SETI Institute collected this signal and they, hopefully, will tell us what the celestial source is. [Update: This thread confirmed the signal source to be the Kepler 4b star.]
Some important questions about the FSK modulated signal:
- Is the signal's proximity of -500 kHz to hydrogen significant or is it an aliasing artifact?
- Are the other tones related in any way? (harmonically or temporally)
- Why is the signal drifting at a +0.0132 Hz/second rate? What should it be drifting at?
- Why is it undergoing a random walk?
- Why are the mark and space frequencies so close together? (1.2 Hz)
- Why is the 0.5061 baud rate so low?
- Do these modulation parameters match any known modem or system?
- Do the demodulated bits match any known line coding, preamble, or training sequence?
- Why is there not a single run of ones (11) in the bit stream?
- Are there any "interesting" sequences or patterns in the demodulated bits?
- Is there any significance to the Autocorrelation images?
- Will this signal ever be seen or collected again?
[Update: The SETI Institute did a re-observation of the Kepler-4 target and the analysis report is here setiQuest Kepler-4b redux.]
Footnotes
1. Decimating by 4096 has the effect of increasing SNR but with the byproduct of reducing gain. Since baudline uses a 16-bit internal sample size this gain reduction can push any weak signal past the LSB thus truncating it. The +30 dB decimation gain setting improves the quantization SNR which eliminates the potential signal loss problem. Note that SNR has been used twice here in this note but in different contexts.
2. This spectral efficiency is roughly equal to that of a 110 baud Bell 101 FSK modem.
3. A context-free grammar is a Computer Science tool that is used to define a formal language. They are very useful in the design of finite automata. Their reduction ability can simplify a complex repetitive string down to it's basic structure.
4. Non-return-to-zero (NRZ) is a telecommunication line coding technique that is useful for overcoming channel deficiencies and for dealing with clocking or synchronization issues.
5. Yes, "bit wacker" is a technical term.
Footnotes
1. Decimating by 4096 has the effect of increasing SNR but with the byproduct of reducing gain. Since baudline uses a 16-bit internal sample size this gain reduction can push any weak signal past the LSB thus truncating it. The +30 dB decimation gain setting improves the quantization SNR which eliminates the potential signal loss problem. Note that SNR has been used twice here in this note but in different contexts.
2. This spectral efficiency is roughly equal to that of a 110 baud Bell 101 FSK modem.
3. A context-free grammar is a Computer Science tool that is used to define a formal language. They are very useful in the design of finite automata. Their reduction ability can simplify a complex repetitive string down to it's basic structure.
4. Non-return-to-zero (NRZ) is a telecommunication line coding technique that is useful for overcoming channel deficiencies and for dealing with clocking or synchronization issues.
5. Yes, "bit wacker" is a technical term.