The Big Bang is a scientific theory that describes how the universe began from nothingness some 13.7 billion years ago. It started with a silent explosion of matter and energy. This incredible cosmic event was completely silent since there wasn't anything to radiate sound into. After the universe expanded and cooled slightly the physics of pressure were allowed to act. Where there is pressure there can be sound, and the universe began to sing.
Two physicists have created slightly different Big Bang acoustic models of the first million years. Both mathematical simulations utilize the cosmic microwave background (CMB) radiation data from the
WMAP survey project. This CMB data is a glimpse back into time at the early universe's density variations. The changes in density became clumps and nulls which attracted and reflected pressure variations in the hot primordial gas. This was sound and it had a spectrum. Both mathematical simulations use this base spectrum as a starting point to extrapolate into the future and the past. They attempt to answer the question of what the Big Bang and the expanding universe might of sounded like.
The
baudline scientific visualizer was used to analyze these two Big Bang acoustic models.
CramerJohn G. Cramer, Professor of Physics at the University of Washington, used a Mathematica program that generated the sound of the universe's first 760,000 years. He used the WMAP microwave data as input and the formula time
2/3 that approximated the rate of growth of the expanding universe. The frequencies of Cramer's simulations have been increased by a factor of 10
26 so that they would be in the audible range.
The
.wav data files, description of the simulation technique, and an explanation of the physics involved can be found here:
The spectrogram of Cramer's model of the universe's first 760,000 years is below:

The above spectrogram shows a universe that is rich in harmonic content. It begins as a downward exponential sweep that decays into a hiss like noise at the end. Cramer says in the afterword of his paper that "the spectrum of frequencies at which the universe was acting as a resonator has been well measured by BOOMERanG and more recently by WMAP." The strong spectral peaks correspond to a resonating structure.
WhittleMark Whittle, Professor at the University of Virginia, used the WMAP data to model the sound of the universe's first million years. The sound has been transposed up by 50 octaves so that it is in the audible range. A 50 octave increase is equal to the frequency being multiplied by a factor of 2
50. The sound of the Big Bang was extremely low bass.
The
.wav data files, description of the simulation technique, and an explanation of the physics involved can be found here:
The spectrogram of Whittle's model of the universe's first 1,000,000 years is below:

The above spectrogram shows a white noise like universe with harmonic rich nulls that exponentially sweep downward in frequency. At the 500,000 year point the higher frequencies transform into high frequency noise. The Whittle model looks a lot like the Cramer model except instead of pure clean tones there are deep nulls.

What is interesting about the spectral nulls is that they look a lot like room mode acoustics where the wall dimensions determine which frequencies are boosted and which are attenuated. To carry this room mode analogy a little further would suggest that the exponential downward sweep is the result of the walls being pushed apart until the 500,000 year point where the walls dissolve allowing any built up frequencies to slowly diffuse. The tangential modes of a cube shaped room would match this spectrum almost exactly but the axial and oblique modes, although weaker, would add extra non-harmonic spectral content. Fortunately a sphere symmetry can be modeled as a cube with only tangential modes.
HarmonicsThe harmonic structure from the Cramer and Whittle models are very different. In fact they do not have integer ratios and they are not true harmonics at all.
The fundamental of the Whittle modes is an oddball null being strangely offset (see spectrum above). All of the other Whittle harmonic nulls line up nicely if a phantom fundamental is used. Try using baudline's
harmonic bars tool to get an interactive feel for this. Below is a frequency vs. harmonic number plot of the Whittle data that shows a straight line relationship, so the first null is on the line but it is not part of the harmonic progression. Not sure if this anomaly is part of the WMAP data or if it is a simulation artifact. If it is a real and accurate phenomena then it opens up a number of intriguing possibilities and questions.

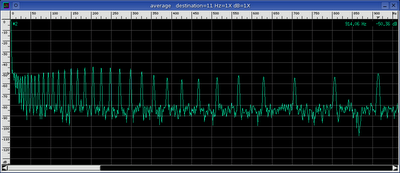
The Cramer spectrum at first looks harmonic in structure but closer examination shows an increasing frequency progression that is almost log like. See the average spectrum below:
 Conclusion
ConclusionThe Cramer and Whittle models are as similar as they are different. They are both interpretations of the same WMAP data and they both demonstrate an almost 14 billion year old sound of the expanding universe. Saying which model is correct is a difficult, if not impossible, task. I can't wait to hear what new data and future physics discoveries might reveal.